Critério da Primeira e Segunda Derivada para Análise
Classificado em Física
Escrito em em  português com um tamanho de 10,88 KB
português com um tamanho de 10,88 KB
| Sinal das Derivadas | Segunda derivada positiva, ou seja,  | Segunda derivada nula, ou seja,  | Segunda derivada negativa, ou seja,  |
|---|---|---|---|
Primeira derivada positiva, ou seja,  | Não é ponto crítico; função é crescente neste ponto e gráfico tem concavidade voltada para cima (ou seja, é uma função convexa no intervalo analisado) | Não é ponto crítico; função é crescente neste ponto | Não é ponto crítico; função é crescente neste ponto e gráfico tem concavidade voltada para baixo (ou seja, é uma função côncava no intervalo analisado) |
Primeira derivada nula, ou seja,  | É ponto crítico; a função atinge um **mínimo local** no ponto  | É ponto crítico; Se a derivada segunda também for nula, não se pode concluir se é ponto de mínimo, máximo ou sela. No entanto, se  for o ponto em questão e se existir algum número for o ponto em questão e se existir algum número 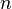 ∈ N tal que ∈ N tal que  se se 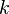 ∈ { ∈ { … … }; };  ≠ ≠  | É ponto crítico; a função atinge um **máximo local** no ponto  |
Primeira derivada negativa, ou seja,  | Não é ponto crítico; função é decrescente neste ponto e gráfico tem concavidade voltada para cima (ou seja, é uma função convexa no intervalo analisado) | Não é ponto crítico; função é decrescente neste ponto | Não é ponto crítico; função é decrescente neste ponto e gráfico tem concavidade voltada para baixo (ou seja, é uma função côncava no intervalo analisado) |
Critério da Derivada de Ordem Superior (f''(x*) = 0)
 tem um **máximo local** em
tem um **máximo local** em  se
se 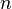 for par e
for par e  ;
; tem um **mínimo local** em
tem um **mínimo local** em  se
se 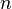 for par e
for par e  ;
; tem um **ponto de inflexão horizontal** em
tem um **ponto de inflexão horizontal** em  se
se 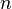 for ímpar.
for ímpar.
Utilizando Derivadas para Esboçar Gráficos de Funções
As derivadas são ferramentas úteis para examinar gráficos de funções. Em particular, os pontos no interior de um domínio de uma função de valores reais que sejam um **extremo local** terão a primeira derivada igual a zero ou a derivada não existirá no ponto: tais pontos são chamados de **pontos críticos**. No entanto, nem todos os pontos críticos são extremos locais. Alguns são **pontos de inflexão**.
A **segunda derivada** é a forma de avaliar esses pontos críticos: se a segunda derivada do ponto crítico é positiva, o ponto é um **mínimo local**; se negativa, é um **máximo local**. Se for nula, o ponto é de inflexão ou parte de uma zona constante (possivelmente ainda um extremo local, mas não necessariamente).
Uma vez que os extremos locais tenham sido encontrados, torna-se geralmente fácil ter uma ideia do gráfico da função, uma vez que (no caso de domínio de uma só dimensão) ela será crescente ou decrescente de forma uniforme, exceto nos pontos críticos, e logo (assumindo que é contínua), terá valores entre os valores nos pontos críticos em cada lado.
