Equivalência de Taxas de Juros Compostos: Guia Completo

Equivalência de Taxas de Juros Compostos

Duas taxas de juros são consideradas equivalentes quando, ao serem aplicadas ao mesmo capital e durante o mesmo intervalo de tempo, produzem o mesmo montante final ou juro. As condições são:

• Serem aplicadas ao mesmo capital;
• Pelo mesmo intervalo de tempo.

No regime de juros compostos, as taxas de juros não são proporcionais. Isso significa que uma taxa de 12% ao ano não é equivalente a 1% ao mês.

Fórmulas de Equivalência

Partindo do princípio acima, se tomarmos um capital inicial (VP) e o aplicarmos a juros compostos pelo período de um ano com uma taxa anual (i_a), teremos o valor futuro (VF):

VF = VP * (1 + i_a)

Se aplicarmos o mesmo capital inicial pelo mesmo período, mas com capitalização mensal a uma taxa mensal (i_m), teremos:

VF = VP * (1 + i_m)¹²

Para que as taxas sejam equivalentes, os montantes devem ser iguais. Assim:

VP * (1 + i_a) = VP * (1 + i_m)¹²

Da igualdade acima, deduz-se a fórmula fundamental da equivalência:

(1 + i_a) = (1 + i_m)¹²

Converter Taxa Mensal para Anual

Para determinar a taxa anual (i_a) a partir de uma taxa mensal (i_m), usa-se a fórmula:

i_a = (1 + i_m)¹² - 1

Converter Taxa Anual para Mensal

Para determinar a taxa mensal (i_m) a partir de uma taxa anual (i_a), a fórmula é:

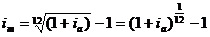
O mesmo raciocínio se aplica para converter taxas mensais ou anuais em taxas diárias, e vice-versa.

Exemplos Práticos

1. Determinar a taxa anual equivalente a 2% ao mês:
   i_a = (1 + i_m)¹² – 1 = (1,02)¹² - 1 = 1,2682 - 1 = 0,2682 ou 26,82%
2. Determinar a taxa mensal equivalente a 60,103% ao ano:
   i_m = (1 + i_a)^1/12 – 1 = (1,60103)^1/12 – 1 = 1,04 - 1 = 0,04 ou 4% ao mês
3. Determinar a taxa anual equivalente a 0,19442% ao dia:
   i_a = (1 + i_d)³⁶⁰ - 1 = (1,0019442)³⁶⁰ - 1 = 2,0122 – 1 = 1,0122 ou 101,22% ao ano (considerando o ano comercial de 360 dias)
4. Determinar a taxa trimestral equivalente a 47,746% em dois anos:
   i_t = (1 + i_2a)^1/8 - 1 = (1,47746)^1/8 - 1 = 1,05 - 1 = 0,05 ou 5% ao trimestre (pois há 8 trimestres em 2 anos)
5. Determinar a taxa anual equivalente a 1% à quinzena:
   i_a = (1 + i_q)²⁴ - 1 = (1,01)²⁴ - 1 = 1,2697 - 1 = 0,2697 ou 26,97% ao ano (pois há 24 quinzenas em 1 ano)

Fórmula Genérica de Equivalência

Como no dia a dia os períodos das taxas podem ser muito variados, podemos usar uma fórmula genérica para qualquer caso:

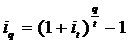
Para facilitar a memorização, as variáveis são definidas como:

• i_q: A taxa para o prazo que eu quero encontrar.
• i_t: A taxa para o prazo que eu tenho.
• q: O número de dias do prazo que eu quero.
• t: O número de dias do prazo que eu tenho.

Vejamos a aplicação da fórmula genérica com mais exemplos:

6. Determinar a taxa para 183 dias, equivalente a 65% ao ano:
   i₁₈₃ = (1 + 0,65)^183/360 – 1 = 28,99%
7. Determinar a taxa para 491 dias, equivalente a 5% ao mês:
   i₄₉₁ = (1 + 0,05)^491/30 – 1 = 122,23%
8. Determinar a taxa para 27 dias, equivalente a 13% ao trimestre:
   i₂₇ = (1 + 0,13)^27/90 – 1 = 3,73%