Exercícios de Cálculo: Derivadas, Integrais e Aplicações

Classificado em Matemática

Escrito em 12 de Novembro de 2025 em português com um tamanho de 12,09 KB

Exercícios de Cálculo com Gabarito

Questão 1 (Ref.: 201601680352)

Com base no gráfico da função f(x) apresentado, analise a composição de funções f(f(a)).

Gráfico de uma função para análise

f(f(a)) está no eixo y > 0
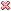f(f(a)) está no eixo y
f(f(a)) está no eixo x > 0
f(f(a)) está no eixo y = 0
f(f(a)) está no eixo x = 0

Questão 2 (Ref.: 201602247738)

Calcule o valor da derivada da função f(x) = (x² - 1) / (x - 1) para x = -5.

Dica: h'(x) = [f'(x)g(x) - f(x)g'(x)] / [g(x)]²

Questão 3 (Ref.: 201601684046)

O proprietário de um estacionamento de veículos verificou que o preço por dia (p) está relacionado com o número de carros diários (x) pela expressão: 10p + 3x = 300. Qual é a receita máxima diária que pode ser obtida?

R$ 810,00
R$ 720,00
R$ 630,00
R$ 480,00
R$ 750,00

Questão 4 (Ref.: 201601685565)

Divida o número 120 em duas partes de forma que o produto de uma pelo quadrado da outra seja máximo.

50 e 70
80 e 40
60 e 60
30 e 90
100 e 20

Questão 5 (Ref.: 201601911686)

Um balão, que mantém sua forma esférica ao ser inflado, tem seu raio aumentando a uma taxa constante de 0,05 m/s. Calcule a taxa de variação do seu volume no instante em que o raio é de 2 m.

0,8π m³/s
0,28π m³/s
0,08π m³/s
0,008π m³/s
1,0π m³/s

Questão 6 (Ref.: 201601685606)

Um ponto de tangente horizontal ao gráfico de y = f(x) ocorre quando a derivada é nula, ou seja, f'(x) = 0. Considerando a função y = x + 1/x, é possível afirmar que:

O gráfico da função não possui ponto de tangente horizontal.
O único ponto de tangente horizontal ao gráfico da função possui coordenadas iguais a (-1, -2).
Os pontos de tangente horizontal ao gráfico da função possuem coordenadas iguais a (1, 2) e (-1, -2).
O único ponto de tangente horizontal ao gráfico da função possui coordenadas iguais a (1, 2).
Existem três pontos de tangente horizontal ao gráfico da função.

Questão 7 (Ref.: 201601682931)

Uma cisterna em forma de cone circular reto invertido tem diâmetro da base de 4 m e altura de 4 m. A cisterna está sendo abastecida com água a uma vazão de 2 m³/min. Encontre a taxa de elevação do nível da água quando este está a 1 m da borda.

(Dado: O volume do cone é V = (1/3)πr²h)

dh/dt = 4/(3π)
dh/dt = 8/(9π)
dh/dt = (9π)/4
dh/dt = (32π)/9
dh/dt = 2/(3π)

Questão 8 (Ref.: 201601727398)

São comuns as interpretações geométrica e trigonométrica da derivada. Geometricamente, a derivada em um ponto x₀ representa o coeficiente angular da reta tangente à curva da função y = f(x) nesse ponto. Trigonometricamente, seu valor é igual à tangente do ângulo que essa reta forma com o eixo x. Diante do exposto, assinale a alternativa verdadeira:

A afirmativa deixa clara a importância de se definir a derivada em um ponto x₀ e este valor calculado é o mesmo para qualquer outro ponto da mesma função variável periódica.
É importante deixar claro que não são duas interpretações independentes como parece, mas são formas de interpretar que se complementam.
A afirmativa deixa clara a importância de se definir derivada em um ponto x₀, ou seja, a taxa de variação instantânea em qualquer ponto de um fenômeno físico variável representado por uma função matemática.
A afirmativa deixa clara a importância de se definir derivada em um ponto x₀ de uma função matematicamente representada de um fenômeno físico.
É importante deixar claro que são duas interpretações independentes.

Questão 9 (Ref.: 201601682954)

Considere a integral I = ∫₀³ (dx)/(x-1) e as afirmativas a seguir:

I é uma integral imprópria divergente.
I é uma integral imprópria convergente para L = ln(2).
I é uma integral definida, sendo I = ln(2).

Assinale a opção correta:

(ii) é verdadeira, (i) e (iii) são falsas.
(i) é verdadeira, (ii) e (iii) são falsas.
(i) é falsa, (ii) e (iii) são verdadeiras.
(iii) é verdadeira, (i) e (ii) são falsas.
(i) e (iii) são verdadeiras, (ii) é falsa.

Questão 10

Considere as funções f(x) = (ln x) / eˣ e g(x) = (ln x)³. Calcule a derivada da soma f(x) + g(x) no ponto x = 1.

Resolução:

$(f(x)+g(x))' = f'(x)+g'(x) \\ \text{em x=1}\\\\ \boxed{(f(1)+g(1))' = f'(1)+g'(1) }$

Temos:

$f(x)= \frac{ln(x)}{e^x} \\\\f'(x)= \frac{(ln(x))'*e^x - ln(x)*(e^x)'}{(e^x)^2} \\\\f'(x)= \frac{ \frac{1}{x}*e^x-ln(x)*e^x }{(e^x)^2} \\\\f'(1)= \frac{1*e^1-ln(1)*e^1}{(e^1)^2} = \frac{e}{e^2} = \frac{1}{e}$

$g(x)=(ln(x))^3\\\\g'(x)=3*(ln(x))^{3-1}*(ln(x))'\\\\g'(x)=3(ln(x))^2 * \frac{1}{x} \\\\g'(1)=3*(ln(1))^2* \frac{1}{1} =0$

A derivada da soma em x=1 é:

$\boxed{\boxed{(f(1)+g(1))' = \frac{1}{e}+0 = \frac{1}{e} }}$

Entradas relacionadas:

Etiquetas: