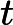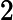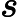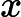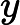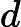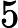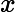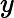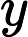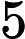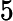Exercícios Resolvidos de Equações Diferenciais

Classificado em Matemática

Escrito em 17 de Julho de 2024 em português com um tamanho de 47,21 KB.

Determine a ordem da equação diferencial abaixo e diga se ela é linear ou não.

y(4)+y(3)+y(2)+y´+y=1

3ª ordem e linear.

5ª ordem e linear.

3ª ordem e não linear.

4ª ordem e linear.

4ª ordem e não linear.

2^a Questão (Ref.:201604369665)

Pontos: 0,1 / 0,1

Marque a alternativa que indica a solução geral da equação diferencial de variáveis separáveis dx + e^3xdy.

y = (e^-3x/3) + k

y = e^-3x + K

y = e^-2x+ k

y = (e^3x/2) + k

y = (e^-2x/3) + k

3^a Questão (Ref.:201604369726)

Pontos: 0,1 / 0,1

Grandezas Vetoriais e Escalares

São grandezas vetoriais, exceto:

Um corpo em queda livre.

Maria assistindo um filme do arquivo X.

João dirigindo o seu carro indo em direção ao bairro do Riacho Fundo.

O avião da Air France partindo do aeroporto de Brasília com destino a Paris.

Maria indo se encontrar com João, na porta do cinema.

4^a Questão (Ref.:201604369695)

Pontos: 0,1 / 0,1

Resolvendo a equação diferencial (x+1)y'' = x + 6, encontramos:

y = x + 4 ln| x + 1 | + C

y = -x + 5 ln | x + 1 | + C

y = -3x + 8 ln | x - 2 | + C

y = ln | x - 5 | + C

y = x + 5 ln | x + 1 | + C

5^a Questão (Ref.:201604369634)

Pontos: 0,1 / 0,1

Determine o limite da função (t² , cos t, t³) parametrizada quando t tende a zero.

(1,1,1)

(0,1,0)

Determinando na equação diferencial abaixo a sua ordem e o seu grau encontramos:
y"+3y''+6y=sen(x)

ordem 2 grau 2

ordem 1 grau 1

ordem 1 grau 3

ordem 1 grau 2

ordem 2 grau 1

2^a Questão (Ref.:201604369685)

Pontos: 0,1 / 0,1

Marque a alternativa que indica a solução da equação y" + 4y = 0.

y = C₁cos2t + C₂sen2t

3^a Questão (Ref.:201604369736)

Pontos: 0,1 / 0,1

Determine a ordem e o grau da equação diferencial abaixo:

$0074.png?V=2.7.0$ $0032.png?V=2.7.0$ $0073.png?V=2.7.0$ $0028.png?V=2.7.0$ $0032.png?V=2.7.0$ $0029.png?V=2.7.0$ $2212.png?V=2.7.0$ $0074.png?V=2.7.0$ $0073.png?V=2.7.0$ $003D.png?V=2.7.0$ $0031.png?V=2.7.0$ $2212.png?V=2.7.0$ $0073.png?V=2.7.0$ $0065.png?V=2.7.0$ $006E.png?V=2.7.0$ $0028.png?V=2.7.0$ $0074.png?V=2.7.0$ $0029.png?V=2.7.0$ t2s(2)−ts=1−sen(t)

Ordem 2 e grau 1.

4^a Questão (Ref.:201604369744)

Pontos: 0,1 / 0,1

Determinando na equação diferencial abaixo a sua ordem e o seu grau encontramos:
(y")³+3y''+6y=tan(x)

ordem 2 grau 3

5^a Questão (Ref.:201604369731)

Pontos: 0,1 / 0,1

Dadas as EDOs abaixo, determine quais são exatas.

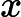
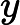
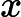
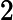
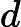
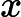
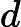
I - $0028.png?V=2.7.0$ $0078.png?V=2.7.0$ $0079.png?V=2.7.0$ $002B.png?V=2.7.0$ $0078.png?V=2.7.0$ $0032.png?V=2.7.0$ $0029.png?V=2.7.0$ $0064.png?V=2.7.0$ $0078.png?V=2.7.0$ $002B.png?V=2.7.0$ $0028.png?V=2.7.0$ $2212.png?V=2.7.0$ $0035.png?V=2.7.0$ $0029.png?V=2.7.0$ $0064.png?V=2.7.0$ $0079.png?V=2.7.0$ $003D.png?V=2.7.0$ $0030.png?V=2.7.0$ (xy+x2)dx+(−5)dy=0

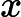
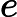
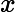
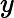
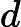
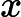
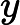
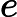
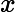
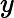
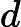
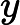
II - 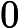$0078.png?V=2.7.0$ $0065.png?V=2.7.0$ $0078.png?V=2.7.0$ $0079.png?V=2.7.0$ $0064.png?V=2.7.0$ $0078.png?V=2.7.0$ $002B.png?V=2.7.0$ $0079.png?V=2.7.0$ $0065.png?V=2.7.0$ $0078.png?V=2.7.0$ $0079.png?V=2.7.0$ $0064.png?V=2.7.0$ $0079.png?V=2.7.0$ $003D.png?V=2.7.0$ $0030.png?V=2.7.0$ xexydx+yexydy=0

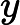
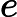
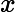
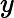
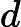
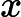
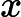
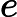
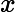
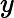
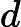
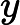
III - 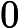$0079.png?V=2.7.0$ $0065.png?V=2.7.0$ $0078.png?V=2.7.0$ $0079.png?V=2.7.0$ $0064.png?V=2.7.0$ $0078.png?V=2.7.0$ $002B.png?V=2.7.0$ $0078.png?V=2.7.0$ $0065.png?V=2.7.0$ $0078.png?V=2.7.0$ $0079.png?V=2.7.0$ $0064.png?V=2.7.0$ $0079.png?V=2.7.0$ $003D.png?V=2.7.0$ $0030.png?V=2.7.0$ yexydx+xexydy=0

Apenas a III.

roblemas de variação de temperatura : A lei de variação de temperatura de Newton afirma que a taxa de variação de temperatura de um corpo é proporcional à diferença de temperatura entre o corpo e o meio ambiente, dT/dt = k( T- T_m) Supondo que um objeto à temperatura inicial de 50⁰F é colocado ao ar livre , onde a temperatura ambiente é de 100 ⁰ F . Se após 5 minutos a temperatura do objeto é de 60 ^oF , determinar a temperatura do corpo após 20 min.

0 graus F

20 graus F

79,5 graus F

-5 graus F

49,5 graus F

3^a Questão (Ref.:201604369693)

Pontos: 0,1 / 0,1

Dada uma função de modo que f(5,6)=7 e seu grau é igual a 1, podemos afirmar que f(20,24) é:

4^a Questão (Ref.:201604369725)

Pontos: 0,1 / 0,1

São grandezas escalares, exceto:

A espessura da parede da minha sala é 10cm.

João empurrando um carrinho de mão, cheio de livros.

5^a Questão (Ref.:201604369639)

Pontos: 0,1 / 0,1

Identifique no intervalo[ - π,π] onde as funções {t,t2, t3} são lineramente dependentes.

t=0

Marque a alternativa que indica a solução geral da equação diferencial de variáveis separáveis

$0079.png?V=2.7.0$ $00B4.png?V=2.7.0$ $003D.png?V=2.7.0$ $0035.png?V=2.7.0$ $0079.png?V=2.7.0$ y´=5y

Nenhuma das alternativas

$0079.png?V=2.7.0$ $003D.png?V=2.7.0$ $0063.png?V=2.7.0$ $0065.png?V=2.7.0$ $0078.png?V=2.7.0$ y=cex

$0079.png?V=2.7.0$ $003D.png?V=2.7.0$ $0063.png?V=2.7.0$ $0065.png?V=2.7.0$ $0035.png?V=2.7.0$ $0078.png?V=2.7.0$ y=ce5x

Entradas relacionadas:

Etiquetas: