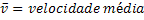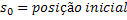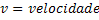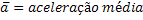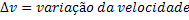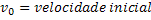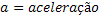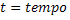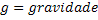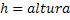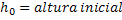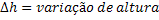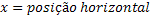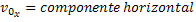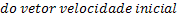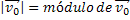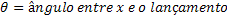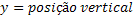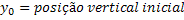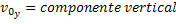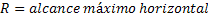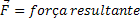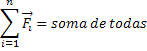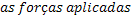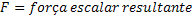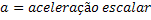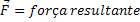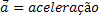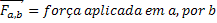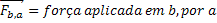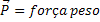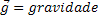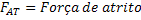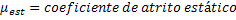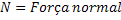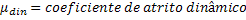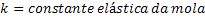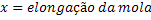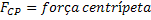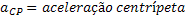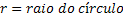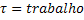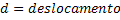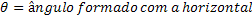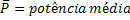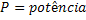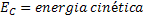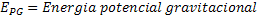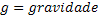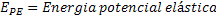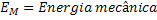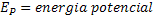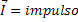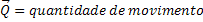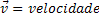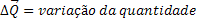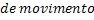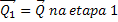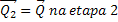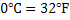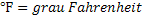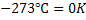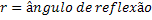Fórmulas e Conceitos Essenciais de Física
Classificado em Física
Escrito em em  português com um tamanho de 123,68 KB
português com um tamanho de 123,68 KB
Cinemática
Velocidade | ||
Velocidade Média | 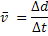 |
|
Movimento Uniforme | ||
Função Horária do Deslocamento | 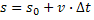 |
|
Movimento Uniformemente Variado (MUV) | ||
Aceleração Média | 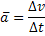 |
|
Função Horária da Velocidade | 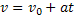 |
|
Função Horária da Posição em Função do Tempo | 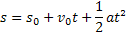 |
|
Equação de Torricelli | 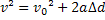 |
|
Movimento Vertical | ||
Função Horária da Velocidade no Movimento Vertical | 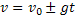 |
|
Função Horária da Posição em Função do Tempo no Movimento Vertical | 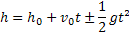 |
|
Equação de Torricelli no Movimento Vertical | 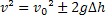 |
|
Movimento Oblíquo | ||
Função Horária da Posição Horizontal | 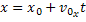 |
|
Componente Horizontal da Velocidade Inicial | 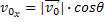 |
|
Função Horária da Posição Vertical | 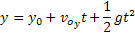 |
|
Componente Vertical da Velocidade Inicial | 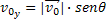 |
|
Alcance Máximo do Projétil Horizontalmente | 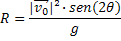 |
|
Dinâmica
Leis de Newton | ||
Força Resultante | 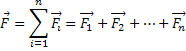 |
|
1ª Lei de Newton (Inércia) | Um corpo em movimento tende a permanecer em movimento e um corpo em repouso tende a permanecer em repouso. | |
2ª Lei de Newton (Princípio Fundamental) | 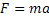 |
|
2ª Lei de Newton Vetorial | 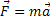 |
|
3ª Lei de Newton (Ação e Reação) | 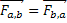 |
|
Força Peso | ||
Peso de um Corpo | 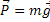 |
|
Força de Atrito | ||
Força de Atrito Estático | 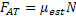 |
|
Força de Atrito Dinâmico | 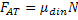 |
|
Força Elástica | ||
Lei de Hooke | 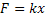 |
|
Força Centrípeta | ||
Força Centrípeta | 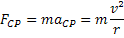 |
|
Trabalho de uma Força | ||
Trabalho | 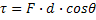 |
|
Potência | ||
Potência Média | 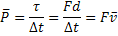 |
|
Potência Instantânea | 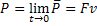 |
|
Energia | ||
Energia Cinética | 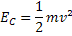 |
|
Energia Potencial Gravitacional | 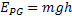 |
|
Energia Potencial Elástica | 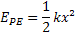 |
|
Energia Mecânica | 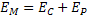 |
|
Impulso e Quantidade de Movimento | ||
Impulso | 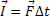 |
|
Quantidade de Movimento | 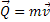 |
|
Teorema do Impulso | 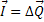 |
|
Conservação da Quantidade de Movimento | 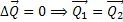 |
|
Termometria
Escalas Termométricas | ||
Escala Celsius | 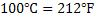 | |
Escala Fahrenheit |
|
|
Escala Kelvin |
|
|
Conversões entre Escalas | ||
Celsius para Fahrenheit | 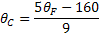 |
|
Fahrenheit para Celsius | 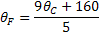 |
|
Celsius para Kelvin | 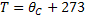 |
|
Kelvin para Celsius | 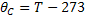 |
|
Óptica
Refração da Luz | ||
Lei da Refração | 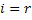 |
|
Ondas
Classificação das Ondas
Uma onda é um movimento causado por uma perturbação, e esta se propaga através de um meio.
Um exemplo de onda é quando se joga uma pedra em um lago de águas calmas, onde o impacto causará uma perturbação na água, fazendo com que ondas circulares se propaguem pela superfície da água.

Também existem ondas que não podemos observar a olho nu, como, por exemplo, ondas de rádio, ondas de televisão, ondas ultravioleta e micro-ondas.
Além destas, existem alguns tipos de ondas que conhecemos bem, mas que não identificamos normalmente, como a luz e o som.
Mas o que elas têm em comum é que todas são energias propagadas através de um meio, e este meio não acompanha a propagação.
Conforme sua natureza, as ondas são classificadas em:
- Ondas Mecânicas: são ondas que necessitam de um meio material para se propagar, ou seja, sua propagação envolve o transporte de energia cinética e potencial e depende da elasticidade do meio. Por isso, não são capazes de se propagar no vácuo. Alguns exemplos são as ondas em molas e cordas, o som e as ondas em superfícies de líquidos.
- Ondas Eletromagnéticas: são ondas geradas por cargas elétricas oscilantes e sua propagação não depende do meio em que se encontram, podendo propagar-se no vácuo e em determinados meios materiais. Alguns exemplos são as ondas de rádio, de radar, os raios X e as micro-ondas.
Todas as ondas eletromagnéticas têm em comum a sua velocidade de propagação no vácuo, próxima a 300.000 km/s, que é equivalente a 1.080.000.000 km/h.
Por que as ondas do mar quebram? Sabendo que as ondas em geral têm como característica fundamental propagar energia sem que haja movimentação do meio, como se explica o fenômeno de quebra das ondas do mar, causando movimentação de água próximo à costa? Em águas profundas, as ondas do mar não transportam matéria, mas ao se aproximarem da costa, há uma brusca diminuição da profundidade onde se encontram, provocando a quebra dessas ondas e causando uma movimentação de toda a massa de água e a formação de correntezas. Após serem quebradas, as ondas do mar deixam de se comportar como ondas. |
Quanto à direção de propagação, as ondas são classificadas como:
- Unidimensionais: que se propagam em apenas uma direção, como as ondas em cordas e molas esticadas;
- Bidimensionais: são aquelas que se propagam por uma superfície, como as ondas na água de um lago quando se joga uma pedra;
- Tridimensionais: são capazes de se propagar em todas as dimensões, como a luz e o som.
Quanto à direção da vibração, as ondas podem ser classificadas como:
- Transversais: são as que são causadas por vibrações perpendiculares à propagação da onda, como, por exemplo, em uma corda:
- Longitudinais: são ondas causadas por vibrações com a mesma direção da propagação, como as ondas sonoras.
Componentes de uma Onda
Uma onda é formada por alguns componentes básicos que são:
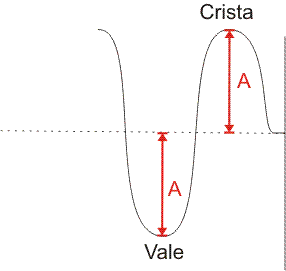
Sendo A a amplitude da onda.
É denominado comprimento de onda, e expresso pela letra grega lambda (λ), a distância entre duas cristas ou dois vales consecutivos.
Chamamos período da onda (T) o tempo decorrido até que duas cristas ou dois vales consecutivos passem por um ponto e frequência da onda (f) o número de cristas ou vales consecutivos que passam por um mesmo ponto, em uma determinada unidade de tempo.
Portanto, o período e a frequência são relacionados por:
A unidade internacionalmente utilizada para a frequência é Hertz (Hz), sendo que 1 Hz equivale à passagem de uma crista ou de um vale em 1 segundo.
Para o estudo de ondas bidimensionais e tridimensionais, são necessários os conceitos de:
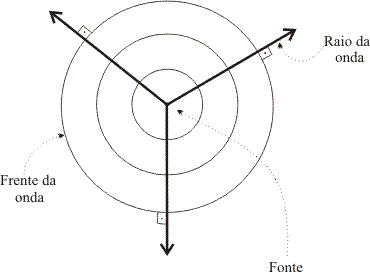
- Frente de Onda: é a fronteira da região ainda não atingida pela onda com a região já atingida;
- Raio de Onda: é possível definir como o raio de onda a linha que parte da fonte e é perpendicular às frentes de onda, indicando a direção e o sentido de propagação.
Velocidade de Propagação das Ondas
Como não transportam matéria em seu movimento, é previsível que as ondas se desloquem com velocidade contínua; logo, estas devem ter um deslocamento que valide a expressão:
Que é comum aos movimentos uniformes, mas conhecendo a estrutura de uma onda:
Podemos considerar que ΔS = λ e que Δt = T.
Assim:
Sendo esta a equação fundamental da Ondulatória, já que é válida para todos os tipos de onda.
É comum utilizarem-se frequências na ordem de kHz (1 quilohertz = 1.000 Hz) e de MHz (1 megahertz = 1.000.000 Hz).
Reflexão de Ondas
É o fenômeno que ocorre quando uma onda incide sobre um obstáculo e retorna ao meio de propagação, mantendo as características da onda incidente.
Independentemente do tipo de onda, o módulo da sua velocidade permanece inalterado após a reflexão, já que ela continua se propagando no mesmo meio.
Reflexão em Ondas Unidimensionais
Esta análise deve ser dividida em oscilações com extremidade fixa e com extremidade livre:
Com Extremidade Fixa:
Quando um pulso (meia-onda) é gerado, faz cada ponto da corda subir e depois voltar à posição original. No entanto, ao atingir uma extremidade fixa, como uma parede, a força aplicada nela, pelo princípio da ação e reação, reage sobre a corda, causando um movimento na direção da aplicação do pulso, com um sentido inverso, gerando um pulso refletido. Assim como mostra a figura abaixo:
Para este caso, costuma-se dizer que há inversão de fase, já que o pulso refletido executa o movimento contrário ao do pulso incidente.
Com Extremidade Livre:
Considerando uma corda presa por um anel a uma haste idealizada, portanto, sem atrito.
Ao atingir o anel, o movimento é continuado, embora não haja deslocamento no sentido do pulso, apenas no sentido perpendicular a este. Então, o pulso é refletido na direção da aplicação, mas com sentido inverso. Como mostra a figura:
Para estes casos, não há inversão de fase, já que o pulso refletido executa o mesmo movimento do pulso incidente, apenas com sentido contrário.
É possível obter a extremidade livre amarrando-se a corda a um barbante muito leve, flexível e inextensível.
Refração de Ondas
É o fenômeno que ocorre quando uma onda passa de um meio para outro de características distintas, tendo sua direção desviada.
Independentemente de cada onda, sua frequência não é alterada na refração; no entanto, a velocidade e o comprimento de onda podem se modificar.
Através da refração, é possível explicar inúmeros efeitos, como o arco-íris, a cor do céu no pôr do sol e a construção de aparelhos astronômicos.
A refração de ondas obedece a duas leis que são:
- 1ª Lei da Refração: O raio incidente, a reta perpendicular à fronteira no ponto de incidência e o raio refratado estão contidos no mesmo plano.
- Lei de Snell: Esta lei relaciona os ângulos, as velocidades e os comprimentos de onda de incidência e refração, sendo matematicamente expressa por:
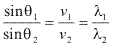
Aplicando a lei:
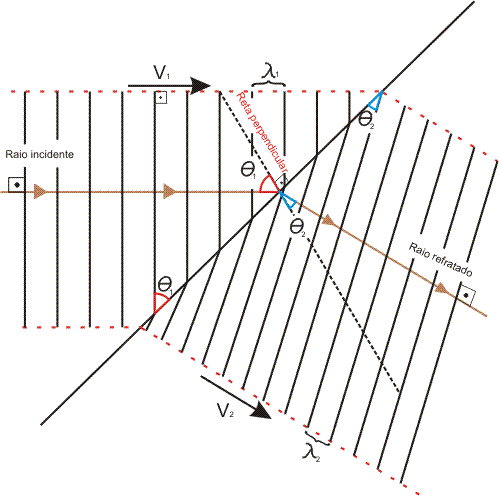
Conforme indicado na figura:
Como exemplos da refração, podem ser usadas ondas propagando-se na superfície de um líquido e passando por duas regiões distintas. É possível verificar experimentalmente que a velocidade de propagação nas superfícies de líquidos pode ser alterada modificando-se a profundidade do local. As ondas diminuem o módulo de velocidade ao se diminuir a profundidade.
Densidade
Pressão Hidrostática
Empuxo
Assim como para os gases, um dos efeitos da variação da temperatura é a variação de dimensões em corpos sólidos e líquidos. Esta variação é o que chamamos Dilatação Térmica.
Dilatação Linear
Aplica-se apenas para os corpos em estado sólido, e consiste na variação considerável de apenas uma dimensão. Como, por exemplo, em barras, cabos e fios.
Ao considerarmos uma barra homogênea, por exemplo, de comprimento a uma temperatura inicial
. Quando esta temperatura é aumentada até uma
(>
), observa-se que esta barra passa a ter um comprimento
(>
).
Com isso, é possível concluir que a dilatação linear ocorre de maneira proporcional à variação de temperatura e ao comprimento inicial . Mas ao serem analisadas barras de dimensões iguais, porém feitas de um material diferente, sua variação de comprimento seria diferente. Isso ocorre porque a dilatação também leva em consideração as propriedades do material com que o objeto é feito; esta é a constante de proporcionalidade da expressão, chamada de coeficiente de dilatação linear (α).
Assim podemos expressar:
A unidade usada para α é o inverso da unidade de temperatura, como: .
Alguns valores usuais de coeficientes de dilatação linear:
| Substância | α (10-6 °C-1) |
| Chumbo | |
| Zinco | |
| Alumínio | |
| Prata | |
| Cobre | |
| Ouro | |
| Ferro | |
| Platina | |
| Vidro (comum) | |
| Tungstênio | |
| Vidro (pyrex) |
Lâmina Bimetálica
Uma das aplicações da dilatação linear mais utilizadas no cotidiano é a construção de lâminas bimetálicas, que consistem em duas placas de materiais diferentes e, portanto, com coeficientes de dilatação linear diferentes, soldadas. Ao serem aquecidas, as placas aumentam seu comprimento de forma desigual, fazendo com que esta lâmina soldada entorte.
As lâminas bimetálicas são encontradas principalmente em dispositivos elétricos e eletrônicos, já que a corrente elétrica causa aquecimento dos condutores, que não podem sofrer um aquecimento maior do que foram construídos para suportar.
Quando a lâmina é curvada, ela tem o objetivo de interromper a corrente elétrica. Após um tempo em repouso, a temperatura do condutor diminui, fazendo com que a lâmina volte ao seu formato inicial e reabilitando a passagem de eletricidade.
Representação Gráfica
Podemos expressar a dilatação linear de um corpo através de um gráfico de seu comprimento (L) em função da temperatura (θ), desta forma:
O gráfico deve ser um segmento de reta que não passa pela origem, já que o comprimento inicial não é igual a zero.
Considerando um ângulo φ como a inclinação da reta em relação ao eixo horizontal, podemos relacioná-lo com:
Pois:
Dilatação Superficial
Esta forma de dilatação consiste em um caso onde há dilatação linear em duas dimensões.
Considere, por exemplo, uma peça quadrada de lados que é aquecida a uma temperatura
, de forma que esta sofra um aumento em suas dimensões. Mas, como há dilatação igual para os dois sentidos da peça, esta continua quadrada, mas passa a ter lados
.
Podemos estabelecer que:
assim como:
E relacionando com cada lado podemos utilizar:
Para que possamos analisar as superfícies, podemos elevar toda a expressão ao quadrado, obtendo uma relação com suas áreas:
Mas a ordem de grandeza do coeficiente de dilatação linear (α) é , o que, ao ser elevado ao quadrado, passa a ter grandeza
, sendo imensamente menor que α. Como a variação da temperatura (Δθ) dificilmente ultrapassa um valor de 10³°C para corpos no estado sólido, podemos considerar o termo α²Δθ² desprezível em comparação com 2αΔθ, o que nos permite ignorá-lo durante o cálculo, assim:
Mas, considerando-se:
Onde β é o coeficiente de dilatação superficial de cada material, tem-se que:
Observe que esta equação é aplicável para qualquer superfície geométrica, desde que as áreas sejam obtidas através das relações geométricas para cada uma em particular (circular, retangular, trapezoidal, etc.).
Transmissão de Calor
Em certas situações, mesmo não havendo o contato físico entre os corpos, é possível sentir que algo está mais quente. Como quando se chega perto do fogo de uma lareira. Assim, concluímos que, de alguma forma, o calor emana desses corpos "mais quentes", podendo se propagar de diversas maneiras.
Como já vimos anteriormente, o fluxo de calor acontece no sentido da maior para a menor temperatura.
Este trânsito de energia térmica pode acontecer das seguintes maneiras:
- Condução;
- Convecção;
- Irradiação.
Fluxo de Calor
Para que um corpo seja aquecido, normalmente, usa-se uma fonte térmica de potência constante, ou seja, uma fonte capaz de fornecer uma quantidade de calor por unidade de tempo.
Definimos fluxo de calor (Φ) que a fonte fornece de maneira constante como o quociente entre a quantidade de calor (Q) e o intervalo de tempo de exposição (Δt):
Sendo a unidade adotada para fluxo de calor, no Sistema Internacional, o Watt (W), que corresponde a Joule por segundo, embora também sejam muito usadas as unidades caloria/segundo (cal/s) e seus múltiplos: caloria/minuto (cal/min) e quilocaloria/segundo (kcal/s).
Capacidade Térmica
É a quantidade de calor que um corpo necessita receber ou ceder para que sua temperatura varie uma unidade.
Então, pode-se expressar esta relação por:
Sua unidade usual é cal/°C.
A capacidade térmica de 1g de água é de 1 cal/°C, já que seu calor específico é 1 cal/g.°C.
Eletrostática
Cargas Elétricas
Toda a matéria que conhecemos é formada por moléculas. Estas, por sua vez, são formadas por átomos, que são compostos por três tipos de partículas elementares: prótons, nêutrons e elétrons.
Os átomos são formados por um núcleo, onde ficam os prótons e nêutrons, e uma eletrosfera, onde os elétrons permanecem em órbita.
Os prótons e nêutrons têm massa praticamente igual, mas os elétrons têm massa milhares de vezes menor. Sendo m a massa dos prótons, podemos representar a massa dos elétrons como:
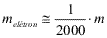
Ou seja, a massa dos elétrons é aproximadamente 2 mil vezes menor que a massa dos prótons.
Podemos representar um átomo, embora fora de escala, por:
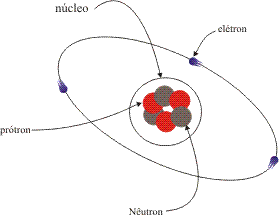
Se pudéssemos separar os prótons, nêutrons e elétrons de um átomo e lançá-los em direção a um ímã, os prótons seriam desviados para uma direção, os elétrons para uma direção oposta à do desvio dos prótons e os nêutrons não seriam afetados.
Esta propriedade de cada uma das partículas é chamada carga elétrica. Os prótons são partículas com cargas positivas, os elétrons têm carga negativa e os nêutrons têm carga neutra.
Um próton e um elétron têm valores absolutos iguais, embora tenham sinais opostos. O valor da carga de um próton ou um elétron é chamado carga elétrica elementar e simbolizado por e.
A unidade de medida adotada internacionalmente para a medida de cargas elétricas é o coulomb (C).
A carga elétrica elementar é a menor quantidade de carga encontrada na natureza. Comparando-se este valor com o coulomb, tem-se a relação:
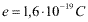
A unidade coulomb é definida partindo-se do conhecimento de densidades de corrente elétrica, medida em ampère (A), já que suas unidades são interdependentes.
Um coulomb é definido como a quantidade de carga elétrica que atravessa, em um segundo, a seção transversal de um condutor percorrido por uma corrente igual a 1 ampère.
Eletrização de Corpos
A única modificação que um átomo pode sofrer sem que haja reações de alta liberação e/ou absorção de energia é a perda ou ganho de elétrons.
Por isso, um corpo é chamado neutro se ele tiver número igual de prótons e de elétrons, fazendo com que a carga elétrica sobre o corpo seja nula.
Pela mesma analogia, podemos definir corpos eletrizados positivamente e negativamente.
Um corpo eletrizado negativamente tem maior número de elétrons do que de prótons, fazendo com que a carga elétrica sobre o corpo seja negativa.
Um corpo eletrizado positivamente tem maior número de prótons do que de elétrons, fazendo com que a carga elétrica sobre o corpo seja positiva.
Fique Atento: É comum haver confusão sobre corpos positivamente carregados, principalmente, já que é plausível pensar que, para que o corpo tenha carga elétrica positiva, ele deva receber carga elétrica positiva, ou seja, ganhar prótons. Quando, na verdade, um corpo está positivamente carregado se ele perder elétrons, ficando com menos carga elétrica negativa. Para que, durante os cálculos, você não se confunda, lembre-se de que a física vista a nível de ensino médio estuda apenas reações elementares e cotidianas, como o movimento de elétrons. As reações onde as partículas intranucleares (nêutrons e prótons) podem ser modificadas são estudadas na parte da ciência conhecida como Física Nuclear. |
Eletrizar um corpo significa basicamente tornar diferente o número de prótons e de elétrons (adicionando ou reduzindo o número de elétrons).
Podemos definir a carga elétrica de um corpo (Q) pela relação:
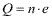
Onde:
- Q = Carga elétrica, medida em coulomb no SI;
- n = Quantidade de cargas elementares, que é uma grandeza adimensional e tem sempre valor inteiro (n = 1, 2, 3, 4...);
- e = Carga elétrica elementar (
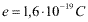 ).
).
A eletrostática é basicamente descrita por dois princípios: o da atração e repulsão de cargas conforme seu sinal (sinais iguais se repelem e sinais contrários se atraem) e o da conservação de cargas elétricas, o qual assegura que, em um sistema isolado, a soma de todas as cargas existentes será sempre constante, ou seja, não há perdas.
Indução Eletromagnética
Quando uma área delimitada por um condutor sofre variação de fluxo de indução magnética, é criada entre seus terminais uma força eletromotriz (fem) ou tensão. Se os terminais estiverem ligados a um aparelho elétrico ou a um medidor de corrente, esta força eletromotriz irá gerar uma corrente, chamada corrente induzida.
Este fenômeno é chamado de indução eletromagnética, pois é causado por um campo magnético e gera correntes elétricas.
A corrente induzida só existe enquanto há variação do fluxo, chamado fluxo indutor.
Eletrodinâmica
Corrente Elétrica
Ao se estudarem situações onde as partículas eletricamente carregadas deixam de estar em equilíbrio eletrostático, passamos à situação onde há deslocamento dessas cargas para uma determinada direção e em um sentido; este deslocamento é o que chamamos corrente elétrica.
Estas correntes elétricas são responsáveis pela eletricidade considerada utilizável por nós.
Normalmente, utiliza-se a corrente causada pela movimentação de elétrons em um condutor, mas também é possível haver corrente de íons positivos e negativos (em soluções eletrolíticas ou gases ionizados).
A corrente elétrica é causada por uma diferença de potencial elétrico (d.d.p./tensão). Ela é explicada pelo conceito de campo elétrico, ou seja, ao considerar uma carga A positiva e outra B negativa, então há um campo orientado da carga A para B. Ao se ligar um fio condutor entre as duas, os elétrons livres tendem a se deslocar no sentido da carga positiva, devido ao fato de terem cargas negativas, lembrando que sinais opostos são atraídos.
Desta forma, cria-se uma corrente elétrica no fio, com sentido oposto ao campo elétrico, e este é chamado sentido real da corrente elétrica. Embora seja convencionado que a corrente tenha o mesmo sentido do campo elétrico, o que não altera em nada seus efeitos (com exceção para o fenômeno chamado Efeito Hall), este é chamado o sentido convencional da corrente.
Para calcular a intensidade da corrente elétrica (i) na seção transversal de um condutor, considera-se o módulo da carga que passa por ele em um intervalo de tempo, ou seja:
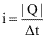
Considerando |Q| = n · e
A unidade adotada para a intensidade da corrente no SI é o ampère (A), em homenagem ao físico francês André-Marie Ampère, e designa coulomb por segundo (C/s).
Sendo alguns de seus múltiplos:
Continuidade da Corrente Elétrica
Para condutores sem dissipação, a intensidade da corrente elétrica é sempre igual, independentemente de sua seção transversal; esta propriedade é chamada continuidade da corrente elétrica.
Isso implica que, se houver "opções de caminho" em um condutor, como por exemplo, uma bifurcação do fio, a corrente anterior a ela será igual à soma das correntes em cada parte desta bifurcação, ou seja:
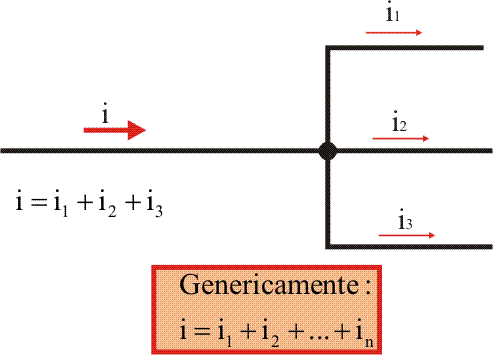
Resistência Elétrica
Ao se aplicar uma tensão U em um condutor qualquer, estabelece-se nele uma corrente elétrica de intensidade i. Para a maior parte dos condutores, estas duas grandezas são diretamente proporcionais, ou seja, conforme uma aumenta, o mesmo ocorre à outra.
Desta forma:
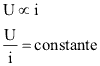
A esta constante chama-se resistência elétrica do condutor (R), que depende de fatores como a natureza do material. Quando esta proporcionalidade é mantida de forma linear, chamamos o condutor de ôhmico, tendo seu valor dado por:
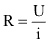
Sendo R constante, conforme enuncia a 1ª Lei de Ohm: Para condutores ôhmicos, a intensidade da corrente elétrica é diretamente proporcional à tensão (d.d.p.) aplicada em seus terminais.
A resistência elétrica também pode ser caracterizada como a "dificuldade" encontrada para que haja passagem de corrente elétrica por um condutor submetido a uma determinada tensão. No SI, a unidade adotada para esta grandeza é o ohm (Ω), em homenagem ao físico alemão Georg Simon Ohm.
Pode-se também definir uma grandeza chamada Condutância elétrica (G), como a facilidade que uma corrente tem em passar por um condutor submetido a determinada tensão, ou seja, este é igual ao inverso da resistência:
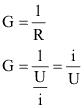
E sua unidade, adotada pelo SI, é o siemens (S), onde:
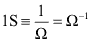
Associação de Resistores
Em um circuito, é possível organizar conjuntos de resistores interligados, chamada associação de resistores. O comportamento desta associação varia conforme a ligação entre os resistores, sendo seus possíveis tipos: em série, em paralelo e mista.
Associação em Série
Associar resistores em série significa ligá-los em um único trajeto, ou seja:

Como existe apenas um caminho para a passagem da corrente elétrica, esta é mantida por toda a extensão do circuito. Já a diferença de potencial entre cada resistor irá variar conforme a resistência deste, para que seja obedecida a 1ª Lei de Ohm, assim:
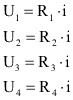
Esta relação também pode ser obtida pela análise do circuito:
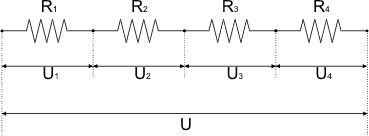
Sendo assim, a diferença de potencial entre os pontos inicial e final do circuito é igual a:
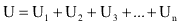
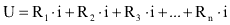
Analisando esta expressão, já que a tensão total e a intensidade da corrente são mantidas, é possível concluir que a resistência total é:
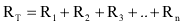
Ou seja, um modo de resumir e lembrar-se das propriedades de um circuito em série é:
| Tensão (d.d.p.) (U) | se divide |
| Intensidade da Corrente (i) | se conserva |
| Resistência Total (R) | soma algébrica das resistências em cada resistor. |
Resistores
São peças utilizadas em circuitos elétricos que têm como principal função converter energia elétrica em energia térmica, ou seja, são usados como aquecedores ou como dissipadores de eletricidade.
Alguns exemplos de resistores utilizados no nosso cotidiano são: o filamento de uma lâmpada incandescente, o aquecedor de um chuveiro elétrico, os filamentos que são aquecidos em uma estufa, entre outros.
Em circuitos elétricos teóricos, costuma-se considerar toda a resistência encontrada proveniente de resistores, ou seja, são consideradas as ligações entre eles como condutores ideais (que não apresentam resistência), e utilizam-se as representações:
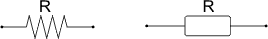
Ímãs e Magnetos
Um ímã é definido como um objeto capaz de provocar um campo magnético à sua volta e pode ser natural ou artificial.
Um ímã natural é feito de minerais com substâncias magnéticas, como por exemplo, a magnetita. Um ímã artificial é feito de um material sem propriedades magnéticas, mas que pode adquirir permanente ou instantaneamente características de um ímã natural.
Os ímãs artificiais também são subdivididos em: permanentes, temporários ou eletroímãs.
- Um ímã permanente é feito de material capaz de manter as propriedades magnéticas mesmo após cessar o processo de imantação; estes materiais são chamados ferromagnéticos.
- Um ímã temporário tem propriedades magnéticas apenas enquanto se encontra sob ação de outro campo magnético; os materiais que possibilitam este tipo de processo são chamados paramagnéticos.
- Um eletroímã é um dispositivo composto de um condutor por onde circula corrente elétrica e um núcleo, normalmente de ferro. Suas características dependem da passagem de corrente pelo condutor; ao cessar a passagem de corrente, cessa também a existência do campo magnético.
Propriedades dos Ímãs
Polos Magnéticos
São as regiões onde se intensificam as ações magnéticas. Um ímã é composto por dois polos magnéticos, norte e sul, normalmente localizados em suas extremidades, exceto quando estas não existirem, como em um ímã em forma de disco, por exemplo. Por esta razão, são chamados dipolos magnéticos.
Para que sejam determinados estes polos, deve-se suspender o ímã pelo centro de massa, e ele se alinhará aproximadamente aos polos norte e sul geográficos, recebendo nomenclatura equivalente. Desta forma, o polo norte magnético deve apontar para o polo norte geográfico e o polo sul magnético para o polo sul geográfico.
Atração e Repulsão
Ao manusear dois ímãs, percebemos claramente que existem duas formas de colocá-los para que estes sejam repelidos e duas formas para que sejam atraídos. Isso se deve ao fato de que polos com o mesmo nome se repelem, mas polos com nomes diferentes se atraem, ou seja:
Esta propriedade nos leva a concluir que os polos norte e sul geográficos não coincidem com os polos norte e sul magnéticos. Na verdade, eles se encontram em pontos praticamente opostos, como mostra a figura abaixo:
A inclinação dos eixos magnéticos em relação aos eixos geográficos é de aproximadamente 191°, fazendo com que seus polos sejam praticamente invertidos em relação aos polos geográficos.
Interação entre Polos
Dois polos se atraem ou se repelem, dependendo de suas características, à razão inversa do quadrado da distância entre eles. Ou seja, se uma força de interação F é estabelecida a uma distância d, ao dobrarmos esta distância, a força observada será igual a uma quarta parte da anterior (F/4). E assim sucessivamente.
Inseparabilidade dos Polos de um Ímã
Esta propriedade diz que é impossível separar os polos magnéticos de um ímã, já que toda vez que este for dividido, serão obtidos novos polos; então, diz-se que qualquer novo pedaço continuará sendo um dipolo magnético.
Campo Magnético
É a região próxima a um ímã que influencia outros ímãs ou materiais ferromagnéticos e paramagnéticos, como cobalto e ferro.
Compare campo magnético com campo gravitacional ou campo elétrico e verá que todos estes têm as características equivalentes.
Também é possível definir um vetor que descreva este campo, chamado vetor indução magnética e simbolizado por 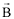 . Se pudermos colocar uma pequena bússola em um ponto sob ação do campo, o vetor
. Se pudermos colocar uma pequena bússola em um ponto sob ação do campo, o vetor 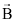 terá a direção da reta em que a agulha se alinha e o sentido para onde aponta o polo norte magnético da agulha.
terá a direção da reta em que a agulha se alinha e o sentido para onde aponta o polo norte magnético da agulha.
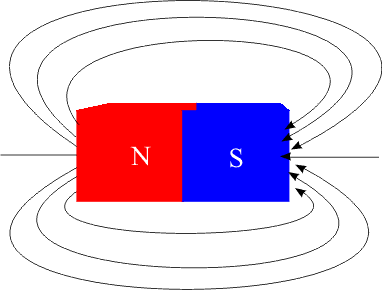
As linhas de indução existem também no interior do ímã; portanto, são linhas fechadas e sua orientação interna é do polo sul ao polo norte. Assim como as linhas de força, as linhas de indução não podem se cruzar e são mais densas onde o campo é mais intenso.
Efeitos de um Campo Magnético sobre Cargas
Como os elétrons e prótons possuem características magnéticas, ao serem expostos a campos magnéticos, interagem com estes, sendo submetidos a uma força magnética 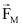 .
.
Supondo:
- Campos magnéticos estacionários, ou seja, que o vetor campo magnético
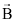 em cada ponto não varia com o tempo;
em cada ponto não varia com o tempo; - Partículas com uma velocidade inicial
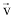 no momento da interação;
no momento da interação; - E que o vetor campo magnético no referencial adotado é
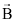 ;
;
Podemos estabelecer pelo menos três resultados:
Carga Elétrica em Repouso
"Um campo magnético estacionário não interage com cargas em repouso."
Tendo um ímã posto sobre um referencial arbitrário R, se uma partícula com carga q for abandonada em sua vizinhança com velocidade nula, não será observado o surgimento de força magnética sobre esta partícula, sendo ela positiva, negativa ou neutra.
Carga Elétrica com Velocidade na Mesma Direção do Campo
"Um campo magnético estacionário não interage com cargas que têm velocidade não nula na mesma direção do campo magnético."
Sempre que uma carga se movimenta na mesma direção do campo magnético, seja no seu sentido ou contrário, não há aparecimento de força eletromagnética que atue sobre ela. Um exemplo deste movimento é uma carga que se movimenta entre os polos de um ímã. A validade desta afirmação é assegurada independentemente do sinal da carga estudada.