Simulado de Métodos Numéricos — 10 Questões

1ª Questão (Ref.:201602653093)

Acerto: 1,0 / 1,0

Arredonde para quatro casas decimais o valor x = 3,1415926536.

• 3,1416
• 3,142
• 3,14159
• 3,1415
• 3,141

2ª Questão (Ref.:201604587616)

Acerto: 1,0 / 1,0

Toda medida física apresenta um erro inerente. Dois erros são muito utilizados para avaliar o afastamento de um valor supostamente correto. Suponha que, ao medir o diâmetro do eixo de um motor, um técnico encontrou o valor 35,42 mm. Ao examinar o manual do motor, a informação é de que o diâmetro deste eixo é 35,50 mm. Qual o erro percentual desta medição?

• 1,08%
• 0,08%
• 8%
• 0,23%
• 0,35%

3ª Questão (Ref.:201602506468)

Acerto: 1,0 / 1,0

Em que intervalo numérico abaixo a função f(x) = x³ - 8x + 1 possui pelo menos uma raiz real?

• (1.5, 2)
• (0, 0.5)
• (0.5, 1)
• (1, 1.5)
• (-0.5, 0)

4ª Questão (Ref.:201604590792)

Acerto: 1,0 / 1,0

Deseja-se buscar a raiz de uma equação f(x) = 0 no intervalo [1,5]. Pelo método da bisseção, o intervalo a ser testado para a raiz na 1ª iteração deve ser escolhido como:

• [1,3] se f(1)·f(3) > 0
• [3,5] se f(3)·f(5) > 0
• [1,3] se f(1)·f(3) < 0
• [1,2] se f(1)·f(2) < 0
• [2,5] se f(2)·f(5) > 0

5ª Questão (Ref.:201602664371)

Acerto: 1,0 / 1,0

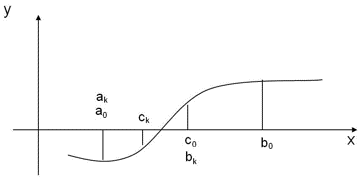
Dentre os métodos numéricos para encontrar raízes (zeros) de funções reais, indique o gráfico que corresponde ao Método do Ponto Fixo:

6ª Questão (Ref.:201602246399)

Acerto: 1,0 / 1,0

Seja a equação P(x) = 0. Se P(1)·P(3) < 0, o Teorema de Bolzano afirma que:

• A equação P(x) = 0 tem uma raiz real no intervalo (1, 3)
• Nada pode-se afirmar a respeito das raízes reais no intervalo (1, 3)
• A equação P(x) = 0 pode ter uma raiz real no intervalo (1, 3)
• A equação P(x) = 0 não tem raiz real no intervalo (1, 3)
• A equação P(x) = 0 tem duas raízes reais no intervalo (1, 3)

7ª Questão (Ref.:201602653927)

Acerto: 1,0 / 1,0

Resolva o sistema de equações abaixo e encontre x₁ e x₂:

5x₁ + 4x₂ = 180

4x₁ + 2x₂ = 120

• x1 = -20 ; x2 = 15
• x1 = 18 ; x2 = 18
• x1 = 10 ; x2 = -10
• x1 = -10 ; x2 = 10
• x1 = 20 ; x2 = 20

8ª Questão (Ref.:201601899789)

Acerto: 1,0 / 1,0

A resolução de sistemas lineares pode ser feita a partir de métodos diretos ou iterativos. Com relação a estes últimos, é correto afirmar, EXCETO, que:

• Consistem em uma sequência de soluções aproximadas
• As soluções do passo anterior alimentam o próximo passo
• Sempre são convergentes
• Apresentam um valor arbitrário inicial
• Existem critérios que mostram se há convergência ou não

Gabarito Comentado

9ª Questão (Ref.:201602665749)

Acerto: 1,0 / 1,0

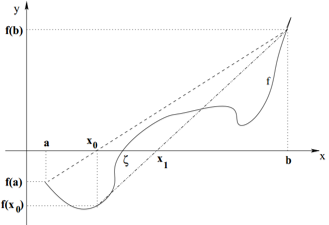
Dentre os métodos numéricos para encontrar raízes (zeros) de funções reais, indique o gráfico que corresponde ao Método das Secantes:

10ª Questão (Ref.:201604597716)

Acerto: 1,0 / 1,0

Numa situação experimental, um engenheiro sabe que o carregamento distribuído sobre uma viga é um arco de parábola dado pela equação W(x) = a·x² + b·x, onde x é dado em metros e W(x) em kN/m. A viga tem comprimento l = 2 m e, nas extremidades, o carregamento é zero. Além disso, no ponto médio da viga W vale 2 kN/m. Encontre a função para W(x).

• W(x) = 2·x² + 4x
• W(x) = x² + 4x
• W(x) = -2·x² + 2x
• W(x) = -x² + 4x
• W(x) = -2·x² + 4x